You are suggested to use the teaching servers burrow.soic.indiana.edu or hulk.soic.indiana.edu or tank.soic.indiana.edu for practicing C programs.
KRUSKAL(G) For each vertex v MakeSet(v) Sort the graph edges into non-decreasing order by their weight cost = 0 For each edge (u,v,weight) taken after the sorting IF FindSet(u) is not equal to FindSet(v) Mark/Print u, v as a minimum spanning tree edge UnionSet(u,v) cost += weight
typedef struct edge_struct
{
int u1;
int u2;
int cost;
} Edge;
#include <stdio.h>
#include <stdlib.h>
typedef struct edge_struct
{
int u1;
int u2;
int cost;
} Edge;
int compare(const void *a, const void *b)
{
return ( ((Edge *)a)->cost - ((Edge *)b)->cost );
}
int main()
{
int i;
int numEdge = 14;
Edge edgeList[14] = {
{0, 1, 4},
{0, 5, 8},
{1, 2, 8},
{1, 5, 11},
{2, 6, 2},
{2, 3, 7},
{2, 8, 4},
{3, 4, 9},
{3, 8, 14},
{4, 8, 10},
{5, 6, 7},
{5, 7, 1},
{6, 7, 6},
{7, 8, 2}
};
qsort(edgeList, numEdge, sizeof(Edge), compare);
for (i = 0; i < numEdge; i++)
printf("%d %d %d\n", edgeList[i].u1, edgeList[i].u2, edgeList[i].cost);
return 0;
}
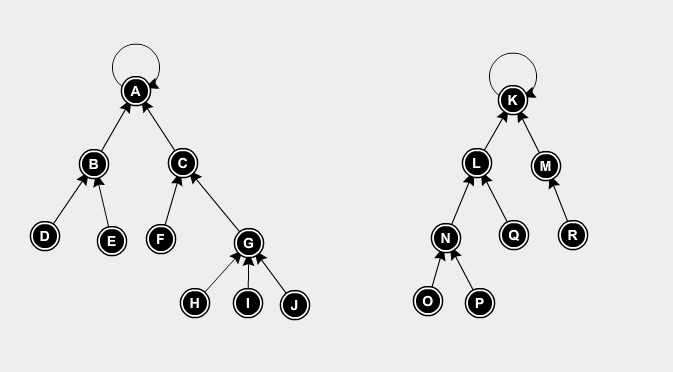
MAKE_SET For all n parent[n] = nEvery set will be represented by the root element. If the elements 1,3,5,6 belongs to the same set all of them would have the same root 1. We can implement the root the following way:
FIND_SET(n) While parent[n] is not equal to n n = parent[n]And finally we can do union operation by assigning the parent of the root of one element as the other element.
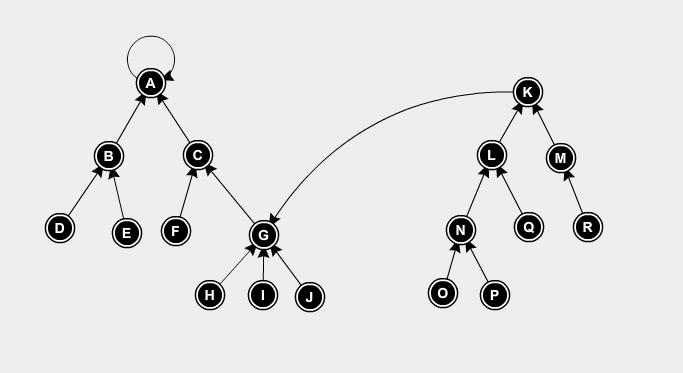
UNION(u, v) parent[FIND_SET(v)] = uIn the illustration below, the arrows points to the parent. All elements from A-J belong to the first set, they all have the same root element A. And all elements from K-R belong to the second set, they all have the same root element K.